初识递归

递归的定义——在一个函数里再调用这个函数本身
递归的最大深度——997

def foo(n):
    print(n)
    n += 1
    foo(n)
foo(1)

997是python为了我们程序的内存优化所设定的一个默认值，我们当然还可以通过一些手段去修改它。


import sys
print(sys.setrecursionlimit(10000))

def foo(n):
    print(n)
    n += 1
    foo(n)

foo(1)

将python允许的递归深度设置为了1w，至于实际可以达到的深度就取决于计算机的性能了。
不推荐修改这个默认的递归深度，因为如果用997层递归都没有解决的问题是不适合使用递归来解决。

汉诺塔问题

从左到右 A B C 柱大盘子在下, 小盘子在上, 借助B柱将所有盘子从A柱移动到C柱, 期间只有一个原则: 大盘子只能在小盘子的下面.

我们只需要考虑如果有64层，先将A柱上的63层移动到B柱上，然后将A柱的第64个移动到C柱上，然后将B柱上的63层移动到C柱上即可。

那怎么把63层都移到B柱上，这个问题可以用上面相同的方法解决。

def move(n,a,b,c):
    if n == 1:
        print(a,'->',c)
    else:
        # 将n-1个胖子从a --> b
        move(n-1,a,c,b)
        # 将剩余的最后一个盘子从a --> c
        print(a,'->',c)
        # 将剩余的n-1个盘子从 b --> c
        move(n-1,b,a,c)

n = int(input('请输入汉诺塔的层数：'))
move(n,'A','B','C')

递归实现三级菜单

menu = {
    '山东': {
        '青岛': ['四方', '黄岛', '崂山', '李沧', '城阳'],
        '济南': ['历城', '槐荫', '高新', '长青', '章丘'],
        '烟台': ['龙口', '莱山', '牟平', '蓬莱', '招远']
    },
    '江苏': {
        '苏州': ['沧浪', '相城', '平江', '吴中', '昆山'],
        '南京': ['白下', '秦淮', '浦口', '栖霞', '江宁'],
        '无锡': ['崇安', '南长', '北塘', '锡山', '江阴']
    },
    '浙江': {
        '杭州': ['西湖', '江干', '下城', '上城', '滨江'],
        '宁波': ['海曙', '江东', '江北', '镇海', '余姚'],
        '温州': ['鹿城', '龙湾', '乐清', '瑞安', '永嘉']
    },
    '安徽': {
        '合肥': ['蜀山', '庐阳', '包河', '经开', '新站'],
        '芜湖': ['镜湖', '鸠江', '无为', '三山', '南陵'],
        '蚌埠': ['蚌山', '龙子湖', '淮上', '怀远', '固镇']
    },
    '广东': {
        '深圳': ['罗湖', '福田', '南山', '宝安', '布吉'],
        '广州': ['天河', '珠海', '越秀', '白云', '黄埔'],
        '东莞': ['莞城', '长安', '虎门', '万江', '大朗']
    },
    '测试': {}
}

def threeLM(dic):
    while True:
        for k in dic:print(k)
        key = input('input>>').strip()
        if key == 'b' or key == 'q':return key
        elif key in dic.keys() and dic[key]:
            ret = threeLM(dic[key])
            if ret == 'q': return 'q'

threeLM(menu)

# l = [menu]
# while l:
#     for key in l[-1]:print(key)
#     k = input('input>>').strip()   # 北京
#     if k in l[-1].keys() and l[-1][k]:l.append(l[-1][k])
#     elif k == 'b':l.pop()
#     elif k == 'q':break

二分查找算法

如果想在列表中查找某个数字，可以排序后从中间开始查找

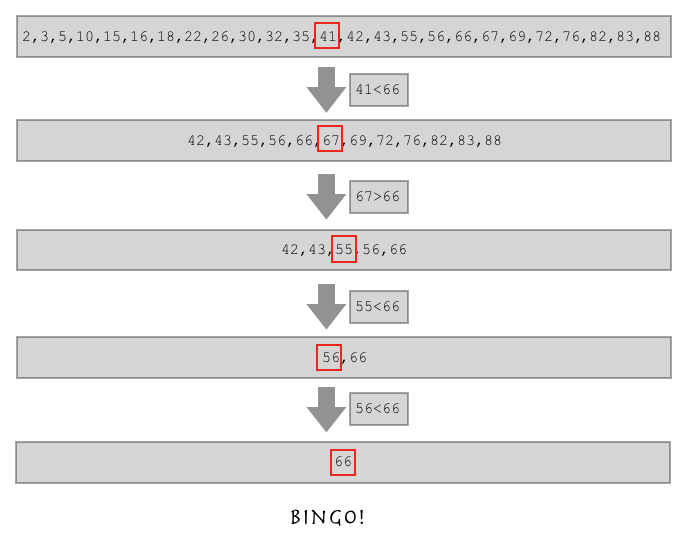
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

# def func(l,aim):
#     mid = (len(l)-1)//2
#     if l:
#         if aim > l[mid]:
#             func(l[mid+1:],aim)
#         elif aim < l[mid]:
#             func(l[:mid],aim)
#         elif aim == l[mid]:
#             print("找到了",mid)
#     else:
#         print('找不到')
# func(l,66)
# func(l,6)

def search(num,l,start=None,end=None):
    start = start if start else 0
    end = len(l)-1 if end is None else end
    mid = (end - start)//2 + start
    if start > end:
        return None
    elif l[mid] > num :
        return search(num,l,start,mid-1)
    elif l[mid] < num:
        return search(num,l,mid+1,end)
    elif l[mid] == num:
        return mid

ret = search(18,l)
print(ret)